
LABORATORIO 11: ARREGLOS
| 11.1 | Introducción |
| 11.2 | Arreglos Unidimensionales (Vectores) |
| 11.3 | Arreglos Bidimensionales (Matrices) |
| 11.4 | Matrices n dimensionales |
| 11.5 | Actividades |
Los arreglos son estructuras de datos conformadas por datos
del mismo tipo. Un arreglo, visto de otra forma, es grupo de posiciones de memoria
relacionadas entre si, por el heccho de que todas se referencian por el mismo
nombre y son del mismo tipo. Para referirse a una posición o un elemento
en particular del arreglo es necesario especificar el nombre del arreglo y el
número de posición del elemento particular dentro del mismo.
11.2 Arreglos Unidimensionales (Vectores)
Los vectores son estructuras de datos que agrupan muchos datos del mismo tipo, en donde cada elemento se puede trabajar individualmente y se puede referenciar con un mismo nombre, a estas estructuras tambien se les llama arreglos unidimensionales, en la Figura 11.1 se muestra la representación simbolica de un vector.
| Vector[0] | Vector[1] | ... |
Vector[n-3] | Vector[n-2] | Vector[n-1] |
Figura 11.1. Estructura de un vector
La forma para declarar un vector en C/C++ es de la siguiente manera :
tipo nombre_vector [ tamaño ];
Ejemplo:
int Vector [ 10 ]; //Declaración de un vector de 10 elementos enteros
Para referenciar un elemento del vector, debe darse un nombre del vector y el indice de la celda que el elemento ocupa en dicho vector. Es importante tener en cuenta que los indices de los vectores empiezan en 0 y terminan en tamaño-1
Ejemplo:
Vector [ 4 ]=526; //Asigna el valor entero 526 al quinto elemento del vector
En general para referenciar un elemento de un vector, en C/C++ se debe colocar así:
nombre_vector [ indice ];
donde indice debe estar entre 0 y tamaño-1
Cabe anotar que al referenciar un elemento de un vector este devuelve el elemento de esa posicion con el tipo del vector Ej:
int elemento;
elemento = Vector [ 4 ];
Fijese que la variable elemento es de tipo entero y vector tambien es entero, esta declaración devuelve el número entero que se encuentra en la posición 5
La forma de llenar de ceros un vector es de la siguiente manera :
for ( indice=0 ; tamano > indice ; indice++){
Vector [ indice ]=0;
}
Alternativamente se podría inicializar el vector, durante la declaración, así:
int Vector[10] = {0};
En lenguaje C/C++ es posible incializar un arreglo con una lista de valores, de la siguiente forma:
int Vector[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
Para leer el elemento i de un vector llamado Vector, se haría así:
scanf("%d",&Vector[i]);
La forma de recorrer un vector es de la siguiente manera:
for ( indice=0 ; tamano > indice ; indice++){ //El
bucle se repite desde 0 hasta el
elemento = vector [ indice ]; // tamaño del vector - 1
Ejemplo 11.1. Llenar cada posicion de un vector de 100 elementos con el valor del indice de cada celda e imprima el vector.

Ejemplo 11.2. Realizar la sumatoria de todos elementos de un vector e imprimir el resultado, cada uno de los elementos del vector se le deben pedir al usuario para llenar dicho vector.

Ejemplo 11.3. Elabore un programa para leer un arreglo cuyos datos se proporcionan en orden ascendente, leer un segundo arreglo cuyos datos se proporcionan en orden descendente, mezclarlos en un tercer arreglo cuyos datos aparezcan en orden ascendente, y por último, imprimir el arreglo resultante.
Solución: Haga clic aquí.
11.3 Arreglos Bidimensionales (Matrices)
Las matrices son estructuras de datos que agrupan muchos datos del mismo tipo, en donde cada elemento se puede trabajar individualmente y se puede referenciar con un mismo nombre, a estas estructuras tambien se les llama arreglos multidimensionales, que contienen filas y columnas. En la Figura 1.2 se muestra la representación simbólica de una matriz.
| matriz[0][0] | matriz[0][1] | matriz[0][2] |
| matriz[1][0] | matriz[1][1] | matriz[1][2] |
| matriz[2][0] | matriz[2][1] | matriz[2][2] |
La forma para declarar una matriz en C/C++ es de la siguiente manera :
tipo nombre_matriz [ tamaño fila ][ tamaño columna ];
Ejemplo:
int Matriz [ 3 ][ 4 ]; //Declara una matriz de 3 filas por 4 columnas.
Para referenciar un elemento de la matriz, debe darse un nombre de la matriz y el indice de la fila y de la columna que el elemento ocupa en dicha matriz. Es importante que los indices de las matrices tanto de las filas como de las columnas empiezan en 0 y terminan en tamaño fila-1 y tamaño columna-1 respectivamente.
En general para referenciar un elemento en C/C++ se debe colocar así:
nombre_matriz [ indice fila ][ indice columna ];
donde indice fila debe estar entre 0 y tamaño fila-1 e indice columna debe estar entre 0 y tamaño columna-1.
Matriz [ 0 ][ 1 ]; //Referencia al segundo elemento de la primera fila
Cabe anotar que al referenciar un elemento de una matriz este devuelve el elemento de esa posición con el tipo de la matriz Ej:
int elemento;
elemento = Matriz [ 0 ][ 1 ];
Fíjese que la variable elemento es de tipo entero y Matriz tambien es entero, esta declaración devuelve el número entero que se encuentra en la fila 0 columna 1
La forma de llenar una matriz de ceros es de la siguiente manera :
for ( fila=0 ; tamanoFila > fila ; fila++){
for ( columna=0 ; tamanoColumna > columna ; columna++){
matriz [ fila ][ columna ] = 0;
}
}
La forma de recorrer una matriz es de la siguiente manera :
for ( fila=0 ; tamanoFila > fila ; fila++){
for ( columna=0 ; tamanoColumna > columna ; columna++){
elemento = matriz [ fila ][ columna ];
}
}
Al declarar una matriz bidimensional, esta puede ser inicializada con un único valor para todos sus elementos, de la siguiente manera:
int B[10][5]={0};//Los 50 elementos de la matriz B se inicializan a cero con esta intrucción
Igualmente a cada uno de los elementos de una matriz se le pueden asignar valores durante de la declaración del arreglo, así:
int A[10][5]={{1,2,3,4,5},{6,7,8,9,10},
{11,12,13,14,15},{16,17,18,19,20},
{21,22,23,24,25},{26,27,28,29,30},
{31,32,33,34,35},{36,37,38,39,40},
{41,42,43,44,45},{46,47,48,49,50}};
Ejemplo 11.4. Elabore un programa que llene una matriz de orden nxn en forma de espiral e imprima la matriz resultante.
Formulación del Problema
Código:
Nombre
Enunciado
Elabore un programa que llene una matriz de orden nxn en forma de espiral e imprima la matriz resultante. Ejemplo: Para n = 5, la matriz resultante sería:
1
2
3
4
5
16
17
18
19
6
15
24
25
20
7
14
23
22
21
8
13
12
11
10
9
Etapas de Resolución del Problema
Fase de Resolución
Análisis del Problema
Descripción:
· Leer el orden de la matriz
· Establecer un ciclo que controle el llenado de la matriz, es decir que controle que los valores asignados a la matriz vayan de 1 a n2, dentro de este ciclo se establecen otros cuatro ciclos apilados (uno se ejecuta después del otro) que corresponden. Cada uno de los ciclos internos va a controlar el llenado de la matriz en un sentido, primero de izquierda a derecha, luego de arriba hacia abajo, el siguiente de izquierda a derecha y por último de abajo hacia arriba, en cada uno de estos ciclos solo se recorre la matriz por una fila o columna, teniendo en cuenta que los valores asignados en el ciclo anterior no los puedo cambiar, es decir que un ciclo no puede recorrer las mismas celdas de la matriz que el ciclo anterior.
· Imprimir la matriz
Datos de Entrada
n: orden de la matriz
Datos de Salida
Matriz llena en forma de espiral
Datos Auxiliares
valor: valores asignados a la matriz, inicio, tope: variables que van a controlar de donde a donde se va llenar la matriz en cada uno de los recorridos, fijo: variable que va controlar el índice de la matriz que no varía durante un recorrido
Diseño y Verificación del Algoritmo
Formalización(Diagramas de Flujo, pseudocódigo)

Fase de
Implementación
Codificación y programa Documentado
Ejecución
11.4 Matrices n dimensionales.
Los arreglos con más de 2 dimensiones se utilizan para el manejo de información que puede ser relacionada por medio de los subíndices, es decir, implícitamente los subíndices contienen información. Un ejemplo de este caso podría la información de una empresa que tiene 4 vendedores que venden 5 productos y para cada uno de los cuales se almacena el total diario de productos vendidos de cada producto durante un mes. La siguiente figura ilustra un posible esquema de almacenamiento para la situación planteada:
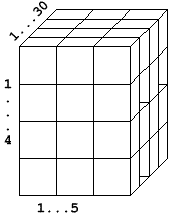
Figura 11.3 Matriz tridimensional
La matriz de la figura se puede interpretar así:
- Las filas corresponden a cada uno de los cuatro vendedores, por lo tanto la fila 1 corresponderá al vendedor 1, la 2 al 2 y así sucesivamente.
- Las columnas corresponden a cada uno de los cinco productos, producto 1 columna 1, producto 2 columna 2...
- La tercera dimensión va a representar los 30 días de un mes, así: índice 1 para el día 1, índice 2 para el día 2, etc.
De acuerdo al esquema planteado la definición del arreglo unidimensional sería:
int Ventas[4][5][30];
Cada elemento se referenciará por cada uno de los 3 subíndices del arreglo, de tal forma que el elemento del arreglo Ventas[0][0][0], corresponderá a las ventas del producto 1, realizadas por el vendedor 1 el dia 1 del mes.
A partir del ejemplo anterior, se podría complementar la estructura agregando una cuarta dimensión para representar los meses, de tal forma que sí esa cuarta dimensión es de 12, el arreglo así definido podría llegar a almacenar las ventas de todo un año en una única estructura, cuya definición sería:
int Ventas[4][5][30][12];
Cabe aclarar, que el orden en el cual se asignen los índices no tiene importancia, siempre y cuando el programa que hace uso de tal estructura sea consistente en el manejo de dichos índices. Es decir, podría haberse definido la estructura así: int Ventas[4][5][12][30] y el manejo sería similar, con la diferencia que ahora el tercer índice será el que represente los meses y el cuarto los días.
Ejemplo 11.5. Escriba un programa que lea las ventas diarias de cada uno de los cinco productos de una empresa, realizadas por cada uno de sus cuatro vendedores durante los 30 días de un mes no determinado. Luego de leer la información esta debe ser procesada para consolidar la siguiente información: total de unidades vendidas de cada producto durante el mes y el producto con el mayor número de unidades vendidas durante un día (indicar producto y día).
Para resolver este problema se va simular el ingreso de datos, dado que el ingreso de datos por teclado implicaría digitar 4*5*30 (600) datos.

Código fuente en programación modular
1. A partir del ejemplo anterior implemente funciones que realicen
lo siguiente: calcular que vendedor vendió la mayor cantidad de productos
durante el mes; el vendedor que realizó la mayor venta diaria; dado un
producto calcular el día en el cual se tuvo la mayor venta de este producto,
imprimir los datos por día, luego por vendedor y luego por producto (la
presentación de los datos debe ser lo más legible posible).
2. Llene cada posicion de un vector de 100 elementos con el valor del indice
de cada celda determinada e imprima el vector.
3 . Busque el mayor y el menor número de un vector con 20 elementos.
4 . Realize la sumatoria de todos elementos de un vector e imprima el resultado,
cada uno de los elementos del vector se le deben pedir al usuario para llenar
dicho vector.
5 . Calcule la media y varianza de los elementos de un vector de enteros utilzando
el metodo anterior (sumatoria). Ayuda : media = Sumatoria (Yi) / n; varianza
= Sumatoria( Yi - media )^2 / n-1
6 . Ordene los elementos de un vector de mayor a menor o al contrario dependiendo
de lo que quiera el usuario.
7 . Llene cada posicion de una matriz con el valor de la suma de la fila y de
la columna correspondiente, los datos deben solicitarsele al usuario.
8 . Realice el promedio de todos elementos de cada fila de una matriz y ese
resultado guardelo en cada posición de un vector, cada uno de los elementos
de la matriz se le deben pedir al usuario para llenar dicha matriz.
9. Realize la suma de dos matrices posición por posición y el
resultado debe quedar en una tercera matriz.
10. Decir si una matriz es triangular superior ( Por debajo de la diagonal que
desciende de izquierda a derecha son ceros ).
11. Llene de un valor dado un rango de una matriz, tanto los elementos iniciales
como el rango y el valor con elcual se rellenará dicho rango son dados
por el usuario.
12. Determine un enunciado para lo que hace el siguiente programa:
#include <stdio.h>
int main()
{
int matriz[5][3], i, j;
for (i = 0; i < 5; i++)
for (j = 0; j < 3; j++)
matriz[i][j] = i + j;
j = 0;
for (i = 0; i < 3; i++)
printf(“%i\n”, matriz[i + j][2 – i]);
return EXIT_SUCCESS;
}
13. Elabore un programa que lea una matriz de m x n y la escriba poniendo las columnas como renglones y los renglones como columnas. Ejemplo: si la matriz leída es:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Entonces al intercambiar columnas y matrices tendríamos:
1 |
6 |
11 |
16 |
2 |
7 |
12 |
17 |
3 |
8 |
13 |
18 |
4 |
9 |
14 |
19 |
5 |
10 |
15 |
20 |
14. Una matriz cuadrada A se dice que es simétrica si
A[i][j] = A[j][i] para todo i, j dentro de los límites de la matriz.
Elabore un programa que lea una matriz y determine si es simétrica o
no.
15. Elabore un programa que lea una matriz de enteros de m x n (1 < n, m
<= 50) y encuentre el menor y el mayor valor y sus posiciones dentro de la
matriz.