ORDENAMIENTO DE VECTORES

3.1 Algoritmos de Ordenamiento Lineal

Por ordenar se entiende el proceso de reorganizar un conjunto de objetos en una cierta secuencia de acuerdo a un criterio especificado. En general, el objetivo de este proceso es facilitar la posterior búsqueda de elementos en el conjunto ordenado.

Existen múltiples ejemplos reales de conjuntos que requieren ser ordenados: la guía telefónica, índices de libros, ficheros de bibliotecas, diccionarios, ficheros de diverso tipo en oficinas, actas de exámenes, etc.

A continuación se describen algunos de los algoritmos de ordenación lineal más conocidos.

3.1.1 BubleSort

La idea de este método es ir tomando los elementos de a dos e ir comparándolos e intercambiándolos de ser necesario, hasta que todos los elementos sean comparados.

for (i=0; i<n-1; i++)
{
   for (j=i+1; j<n; j++)
  {
    if(V[i]>V[j])
    {
     aux = V[i];
     V[i] = V[j];
     V[j] = aux;
    }
  }
}

El bucle externo establece un desplazamiento secuencial dentrodel vector desde el primer elemento hasta el penúltimo , el bucle interno realiza un recorrido del vector desde el elemento i+1 hasta el último elemento del vector y va reduciendo en cada iteración del bucle externo el número de elementos a comparar, ya que los elementos anteriores ya debieron ordenarse en las iteraciones anteriores. Ahora bien, lo que se quiere es ordenar todos los valores, para lo cual se compara el elemento i con los subsiguientes elementos del vector e intercambiándolo cuando sea mayor que alguno de los elementos ubicado en alguna posición inferior del vector, en este intrecambio es que se genera la burbuja, donde los elementos más pequeños van subiendo y los más grandes se van ubicando en las posiciones inferiores del vector.

Ejemplo 3.1. Supongamos que un vector de 10 elementos tiene estos valores:

9 7 6 5 4 3 11 8 10 2

A continuación se describe paso por paso la evolución del método. Representando cada estado del vector de la siguiente manera:

i,j->V[0]V[1]V[2]V[3]V[4]V[5]V[6]V[7]V[8]V[9]

0,1->7 9 6 5 4 3 11 8 10 2
0,2->6 9 7 5 4 3 11 8 10 2
0,3->5 9 7 6 4 3 11 8 10 2
0,4->4 9 7 6 5 3 11 8 10 2
0,5->3 9 7 6 5 4 11 8 10 2
0,6->3 9 7 6 5 4 11 8 10 2
0,7->3 9 7 6 5 4 11 8 10 2
0,8->3 9 7 6 5 4 11 8 10 2
0,9->2 9 7 6 5 4 11 8 10 3
1,2->2 7 9 6 5 4 11 8 10 3
1,3->2 6 9 7 5 4 11 8 10 3
1,4->2 5 9 7 6 4 11 8 10 3
1,5->2 4 9 7 6 5 11 8 10 3
1,6->2 4 9 7 6 5 11 8 10 3
1,7->2 4 9 7 6 5 11 8 10 3
1,8->2 4 9 7 6 5 11 8 10 3
1,9->2 3 9 7 6 5 11 8 10 4
2,3->2 3 7 9 6 5 11 8 10 4
2,4->2 3 6 9 7 5 11 8 10 4
2,5->2 3 5 9 7 6 11 8 10 4
2,6->2 3 5 9 7 6 11 8 10 4
2,7->2 3 5 9 7 6 11 8 10 4
2,8->2 3 5 9 7 6 11 8 10 4
2,9->2 3 4 9 7 6 11 8 10 5
3,4->2 3 4 7 9 6 11 8 10 5
3,5->2 3 4 6 9 7 11 8 10 5
3,6->2 3 4 6 9 7 11 8 10 5
3,7->2 3 4 6 9 7 11 8 10 5
3,8->2 3 4 6 9 7 11 8 10 5
3,9->2 3 4 5 9 7 11 8 10 6
4,5->2 3 4 5 7 9 11 8 10 6
4,6->2 3 4 5 7 9 11 8 10 6
4,7->2 3 4 5 7 9 11 8 10 6
4,8->2 3 4 5 7 9 11 8 10 6
4,9->2 3 4 5 6 9 11 8 10 7
5,6->2 3 4 5 6 9 11 8 10 7
5,7->2 3 4 5 6 8 11 9 10 7
5,8->2 3 4 5 6 8 11 9 10 7
5,9->2 3 4 5 6 7 11 9 10 8
6,7->2 3 4 5 6 7 9 11 10 8
6,8->2 3 4 5 6 7 9 11 10 8
6,9->2 3 4 5 6 7 8 11 10 9
7,8->2 3 4 5 6 7 8 10 11 9
7,9->2 3 4 5 6 7 8 9 11 10
8,9->2 3 4 5 6 7 8 9 10 11

La evolución del método muestra que cada elemento del vector desde el primer elemento hasta el penúltimo se van comparando con los subsiguientes (no con los anteriores), ya que los elementos se han comparado en las iteraciones anteriores

La falencia de este método es que como sí o sí va a hacer n - 1 pasadas, muchas veces puede hacer pasadas inclusive con el vector ya ordenado. Por lo tanto, una mejora para este método consiste en establecer un mecanismo para que verifique cuando el vector este ya ordenado.

Si queremos ordenar el vector descendente cambiamos el signo en la condición del SI por V[i]< V[j].

Análisis del algoritmo.

• 
  Estabilidad: Este algoritmo nunca intercambia registros con claves iguales. Por lo tanto es estable.
• 
  Requerimientos de Memoria: Este algoritmo sólo requiere de una variable adicional para realizar los intercambios sin importar qué tan grande sea el vector. Requerimiento constante.
• 
  Tiempo de Ejecución: El ciclo interno se ejecuta (n-1)*n/2 veces para una lista de n elementos. El ciclo externo se ejecuta n veces. Es decir, la complejidad es n * n = O(n2). El comportamiento del caso promedio depende del orden de entrada de los datos, pero es sólo un poco mejor que el del peor caso, y sigue siendo O(n2).

Este algoritmo es uno de los más pobres en rendimiento. No es recomendable usarlo. Tan sólo está aquí para que sea conocido, y porque su sencillez lo hace bueno para empezar.

3.1.2 SelectionSort

Entre los métodos elementales de ordenación de vectores se encuentra el algoritmo de selección:

for (i=0; i<n; i++)
{
  imin=i;
  for (j=i+1; j<n; j++)
  {
    if(V[j]<V[imin])
    imin=j;
  }
  aux = V[i];
  V[i] = V[imin];
  V[imin] = aux;
}

Es decir, el método se basa en buscar en cada iteracción el mínimo elemento del “subvector” situado entre el índice i y el final del vector e intercambiarlo con el de índice i. Tomando la dimensión del vector n como tamaño del problema es inmediato que el bucle se repite n veces y por tanto la función que da el número de repeticiones es de tipo lineal (O(n)). La operación interior al bucle se puede desarrollar a su vez como:

imin:=i;
para j desde i+1 hasta n hacer
  si V[j]<V[imin] entonces imin:=j fsi
fpara
intercambiar(V[i],V[imin])

Se trata de una secuencia de tres operaciones, la segunda de las cuales es, a su vez, una iteración. La primera (asignación) y la tercera(intercambio) pueden considerarse de coste constante. La segunda es un bucle que internamente incluye una operación condicional que en el peor caso supone una operación de coste constante (O(1)) (en el peor caso y en el mejor, puesto que la comparación se ha de realizar siempre ) y el número de repeticiones de esa operación es de tipo lineal, ya que se realiza n-(i+1) veces, y por tanto, al crecer n, el número de veces crece proporcionalmente a n. Luego será de costeO(n) O(1) = O(n). Éste será entonces el coste de la secuencia completa (sucesión de dos operaciones de coste constante y una de coste lineal)

El algoritmo total será entonces de ordenO(n).O(n) =O(n^2)

Es interesante observar que en este algoritmo el contenido de los datos de entrada, no influye en el coste del algoritmo. En efecto se puede comprobar (aplicar el algoritmo sobre varios vectores ejemplo), que se ejecutan de forma completa ambos bucles tanto para vector desordenado como para vector ordenado.

Ejemplo 3.2. Supongamos que un vector de 10 elementos tiene estos valores:

9 7 6 5 4 3 11 8 10 2

A continuación se describe paso por paso la evolución del método. Representando cada estado del vector de la siguiente manera:

V[i]<->V[imin] =>V[0]V[1]V[2]V[3]V[4]V[5]V[6]V[7]V[8]V[9], igualmente se muestran cada uno de los cambios de la variable imin.

imin -> 1
imin -> 2
imin -> 3
imin -> 4
imin -> 5
imin -> 9
V[0]<->V[9]=>2 7 6 5 4 3 11 8 10 9
imin -> 2
imin -> 3
imin -> 4
imin -> 5
V[1]<->V[5]=>2 3 6 5 4 7 11 8 10 9
imin -> 3

imin -> 4
V[2]<->V[4]=>2 3 4 5 6 7 11 8 10 9
V[3]<->V[3]=>2 3 4 5 6 7 11 8 10 9
V[4]<->V[4]=>2 3 4 5 6 7 11 8 10 9
V[5]<->V[5]=>2 3 4 5 6 7 11 8 10 9
imin -> 7
V[6]<->V[7]=>2 3 4 5 6 7 8 11 10 9
imin -> 8
imin -> 9
V[7]<->V[9]=>2 3 4 5 6 7 8 9 10 11
V[8]<->V[8]=>2 3 4 5 6 7 8 9 10 11
V[9]<->V[9]=>2 3 4 5 6 7 8 9 10 11

Análisis del algoritmo.

• Estabilidad: No es estable. Intercambia registros con claves iguales.
• Requerimientos de Memoria: Este algoritmo sólo requiere de una variable adicional para realizar los intercambios sin importar qué tan grande sea el vector. Requerimiento constante.
• Tiempo de Ejecución: El ciclo externo se ejecuta n veces para una lista de n elementos. Cada búsqueda requiere comparar todos los elementos no clasificados. Luego la complejidad es O(n2). Este algoritmo presenta un comportamiento constante independiente del orden de los datos. Luego la complejidad promedio es también O(n2).

No obstante, ya que sólo realiza un intercambio en cada ejecución del ciclo externo, puede ser una buena opción para listas con registros grandes y claves pequeñas.

3.1.3 InsertionSort

En este procedimiento se recurre a una búsqueda binaria en lugar de una búsqueda secuencial para insertar un elemento en la parte de arriba del arreglo, que ya se encuentra ordenado. El proceso, al igual que en el método de inserción directa, se repite desde el segundo hasta el n-ésimo elemento.

for(i=1; i<n; i++) {
  temp = V[i];
  Izq = 0;
  Der = i-1;
  while(Izq <= Der){
    Medio = (Izq+Der)/2;
    if (temp < V[Medio])
      Der = Medio - 1;
    else
      Izq = Medio + 1;
  }
  for (j=i-1; j>=Izq; j--){
    V[j+1]=V[j];
  }
  V[Izq] = temp;
}

Ejemplo 3.3. Supongamos que un vector de 10 elementos tiene estos valores:

9 7 6 5 4 3 11 8 10 2

A continuación se describe paso por paso la evolución del método. Representando cada estado del vector de la siguiente manera:

i->V[0]V[1]V[2]V[3]V[4]V[5]V[6]V[7]V[8]V[9]
1->7 9 6 5 4 3 11 8 10 2
2->6 7 9 5 4 3 11 8 10 2
3->5 6 7 9 4 3 11 8 10 2
4->4 5 6 7 9 3 11 8 10 2
5->3 4 5 6 7 9 11 8 10 2
6->3 4 5 6 7 9 11 8 10 2
7->3 4 5 6 7 8 9 11 10 2
8->3 4 5 6 7 8 9 10 11 2
9->2 3 4 5 6 7 8 9 10 11

Análisis del algoritmo.

• Estabilidad: Este algoritmo nunca intercambia registros con claves iguales. Por lo tanto es estable.
• Requerimientos de Memoria: Este algoritmo sólo requiere de una variable adicional para realizar los intercambios sin importar qué tan grande sea el vector. Requerimiento constante.
• Tiempo de Ejecución: Al analizar el método de ordenación por inserción binaria se advierte la presencia de un caso antinatural. El método efectúa el menor número de comparaciones cuando el arreglo está totalmente desordenado y el máximo cuando está ordenado.

Es posible suponer que mientras en una búsqueda secuencial se necesitan k comparaciones para insertar un elemento, en una búsqueda binaria se necesitará la mitad de las k comparaciones. Por lo tanto, el número de comparaciones promedio en el método de ordenación por Inserción Binaria puede calcularse como :

C= (1/2) + (2/2) + (3/2) + . . . + ((n-1)/2) = ((n(n-1))/4) = ((n2 – n) / 4)

Éste es un algoritmo de comportamiento antinatural y por lo tanto es necesario ser muy cuidadoso cuando se hace un análisis de él. Las mejoras producen un efecto negativo cuando el arreglo está ordenado y produce resultados apenas satisfactorios cuando las claves (temp y V[Medio]) están desordenadas. De todas maneras debe recordarse que no se reduce el número de movimientos que es una operación más complicada y costosa que la operación de comparación. Por lo tanto, el tiempo de ejecución del algoritmo sigue siendo proporcional a n2.

3.1.4 ShellSort

Denominado así por su desarrollador Donald Shell (1959), ordena una estructura de una manera similar a la del Bubble Sort, sin embargo no ordena elementos adyacentes sino que utiliza una segmentación entre los datos. Esta segmentación puede ser de cualquier tamaño de acuerdo a una secuencia de valores que empiezan con un valor grande (pero menor al tamaño total de la estructura) y van disminuyendo hasta llegar al '1'.

Este método funciona de la siguiente manera:

• Ordena subgrupos de elementos separados K unidades (respecto de su posición en el arreglo) del arreglo original. El valor K es llamado incremento.
• Después de que los primeros K subgrupos han sido ordenados, se escoge un nuevo valor de K más pequeño, y el arreglo es de nuevo partido entre el nuevo conjunto de subgrupos. Cada uno de los subgrupos mayores es ordenado y el proceso se repite de nuevo con un valor más pequeño de K.
• Eventualmente el valor de K llega a ser 1, de tal manera que el subgrupo consiste de todo el arreglo ya casi ordenado.
• Al principio del proceso se escoge la secuencia de decrecimiento de incrementos; el último valor debe ser 1.
• "Es como hacer un ordenamiento de burbuja pero comparando e intercambiando elementos."
• Cuando el incremento toma un valor de 1, todos los elementos pasan a formar parte del subgrupo y se aplica inserción directa.
• El método se basa en tomar como salto N/2 (siendo N el número de elementos) y luego se va reduciendo a la mitad en cada repetición hasta que el salto o distancia vale 1.
  

Algoritmo:

void shellSort(int a[], int h)
{
  int i;
  while (h > 0)
  { for (i = h-1; i<n; i++)
    {
       int B = a[i];
       int j = i;
       for (j = i; (j >= h) && (a[j - h] > B); j -= h)
       { a[j] = a[j - h];}
         a[j] = B;
     }
       h = h / 2;
  }
}

Ejemplo 3.4 Para el arreglo a = [6, 1, 5, 2, 3, 4, 0] tenemos el siguiente recorrido:

Análisis del algoritmo.

• Estabilidad: Este algoritmo se considera estable.
• Requerimientos de Memoria: Una variable adicional para realizar los intercambios. Y una variable para el salto. Requerimiento constante.
• Tiempo de Ejecución: Los estudios realizados indican que su complejidad es de O(n^1.2) en el mejor caso y de O(n^1.25) en el caso promedio.

3.2 Algoritmos de ordenamiento Recursivo

Dentro de los algoritmos de ordenamiento recursivo se encuentran los métodos de MergeSort (Ordenación por mezclas sucesivas) y QuickSort (Ordenamiento Rápido).

3.2.1 MergeSort

El algoritmo Merge divide el arreglo original en dos arreglos y los coloca en arreglos separados. Cada arreglo es recursivamente ordenado y finalmente se unen los arreglos en un arreglo ordenado. Como cualquiera de los algoritmos de ordenamiento recursivo el algoritmo Merge tiene complejidad de O(n log n). Fue desarrollado por John Von Neumann.

Algoritmo

void ordenarMezcla(TipoEle A[], int izq, int der)
{ if ( izq < der )
  { centro = ( izq + der ) % 2;
    ordenarMezcla( A, izq, centro );
    ordenarMezcla( A, centro+1, der);
    intercalar( A, izq, centro, der );
  }
}
void intercalar(TipoEle A[], int a, int c, int b )
{ k = 0;
  i = a;
  j = c + 1;
  n = b - a;
  while ( i < c + 1 ) && ( j < b + 1 )
  { if ( A[i] < A[j] )
    { B[k] = A[i];
      i = i + 1;
    }
    else
    { B[k] = A[j];
      j = j + 1;
    }
   k = k + 1;
  };
while ( i < c + 1 )
{ B[k] = A[i];
  i++;
  k++;
};
while ( j < b + 1 )
{ B[k] = A[j];
  j++;
  k++;
};
i = a;
for ( k = 0; k < n; i++ )
{ A[i] = B[k];
  i++;
};
};

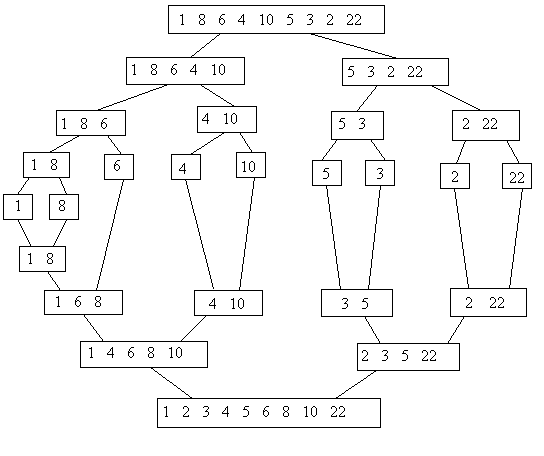
Este método aplica la técnica divide-y-vencerás, dividiendo la secuencia de datos en dos subsecuencias hasta que las subsecuencias tengan un único elemento, luego se ordenan mezclando dos subsecuencias ordenadas en una secuencia ordenada, en forma sucesiva hasta obtener una secuencia única ya ordenada. Si n = 1 solo hay un elemento por ordenar, sino se hace una ordenación de mezcla de la primera mitad del arreglo con la segunda mitad. Las dos mitades se ordenan de igual forma. Ejemplo: Se tiene un arreglo de 8 elementos, se ordenan los 4 elementos de cada arreglo y luego se mezclan. El arreglo de 4 elementos, se ordenan los 2 elementos de cada arreglo y luego se mezclan. El arreglo de 2 elementos, como cada arreglo sólo tiene n = 1 elemento, solo se mezclan.

Ejemplo 3.5 Esquema procedimiento Algoritmo MergeSort

Análisis del algoritmo.

• Estabilidad: Sí es estable.
• Requerimientos de Memoria: Se necesita memoria auxiliar del mismo tamaño de los conjuntos a mezclar.
• Tiempo de Ejecución: O(n log n).
  

  Ventajas	Desventajas
  A) Rápido	A) Implementación compleja.
  B) Especial para datos atómicos o registros con pocos componentes	B) Grandes Requerimientos de Memoria

3.2.2 QuickSort

La ordenacion rapida, inventada y nombrada por C.A.R. Hoare en 1960, esta considerada como el mejor algoritmo de ordenacion disponible actualmente. Esta basada en la ordenacion por el metodo de intercambio.

La ordenacion rápida se basa en la idea de las particiones. El procedimiento general es seleccionar un valor llamado COMPARANDO y entonces dividir el array en dos partes. En un lado todos los elementos mayores o iguales al valor de particion y en otro todos los elementos menores que el valor. Este proceso se repite en cada parte restante hasta que el array esté ordenado.

Como se puede ver, este proceso es esencialmente recursivo por naturaleza y, de hecho, las implementaciones mas claras de la ordenacion rapida es por algoritmos recursivos.

La seleccion del valor comparado se puede obtener de dos formas. Se puede seleccionar aleatoriamente o haciendo la media de un pequeno conjunto de valores tomados del array. Para una ordenacion optima es mejor seleccionar un valor que este precisamente en medio del rango de valores. Sin embargo, esto no es facil de hacer en la mayoria de los conjuntos de datos. En el caso peor, el valor escogido esta en un extremo. Incluso en este, la ordenacion rapida todavia funciona bien. La version de la ordenacion rapida que sigue selecciona el elemento mitad del array. Aunque no siempre sera una buena eleccion, la ordenacion sigue funcionando correctamente.

Ejemplo 3.6 Ordenamiento por QuickSort

Secuencia inicial 8 2 5 3 9
Elemento comparando: 5
Primer paso 3 2 5 8 9
Ahora se ordena con el mismo procedimiento los vectores '3 2' y '8 9'

Algoritmo:

void ordenar (int vect[], int ind_izq, int ind_der)
{
  int i, j; /* variables indice del vector */
  int elem; /* contiene un elemento del vector */
  i = ind_izq;
  j = ind_der;
  elem = vect[(ind_izq+ind_der)/2];
  do
  {while (vect[i] < elem) //recorrido del vector hacia la derecha
    i++;
   while (elem < vect[j]) // recorrido del vector hacia la izquierda
    j--;
   if (i <= j) /* intercambiar */
   { int aux; /* variable auxiliar */
     aux = vect[i];
     vect[i] = vect[j];
     vect[j] = aux;
     i++;
     j--;
   }
  } while (i <= j);
  if (ind_izq < j) {ordenar (vect, ind_izq, j);} //Llamadas recursivas
  if (i < ind_der) {ordenar (vect, i, ind_der);}
}

Análisis del algoritmo.

• Estabilidad: No es estable.
• Requerimientos de Memoria: No requiere memoria adicional en su forma recursiva.
• Tiempo de Ejecución:
  • Caso promedio. La complejidad para dividir una lista de n es O(n). Cada sublista genera en promedio dos sublistas más de largo n/2. Por lo tanto la complejidad se define en forma recurrente como:
    • f(1) = 1
    • f(n) = n + 2 f(n/2)
    • La forma cerrada de esta expresión es: f(n) = n log₂n Es decir, la complejidad es O(n log₂n).
  • El peor caso ocurre cuando la lista ya está ordenada, porque cada llamada genera sólo una sublista (todos los elementos son menores que el elemento de división). En este caso el rendimiento se degrada a O(n²). Con las optimizaciones mencionadas arriba puede evitarse este comportamiento.
  
  

  Ventajas	Desventajas
  A) Generalmente es el más rápido	A) Implementación un poco más complicada
  B) No requiere memoria adicional	B) Mucha diferencia entre el peor (n2) y el mejor caso (log n)
  	C) Intercambia registros iguales

   

RESUMEN.

Eligiendo el más adecuado. No existe EL ALGORITMO de ordenamiento. Sólo existe el mejor para cada caso particular. Debe conocerse a fondo el problema a resolver, y aplicar el más adecuado. Aunque hay algunas preguntas que pueden ayudar a elegir:

¿Qué grado de orden tendrá la información que va a manejar? Si la información va a estar casi ordenada y no desea complicarse, un algoritmo sencillo como el ordenamiento burbuja será suficiente. Si por el contrario los datos van a estar muy desordenados, un algoritmo poderoso como Quicksort puede ser el más indicado. Y si no puede hacer una presunción sobre el grado de orden de la información, lo mejor será elegir un algoritmo que se comporte de manera similar en cualquiera de estos dos casos extremos.

¿Qué cantidad de datos va a manipular? Si la cantidad es pequeña, no es necesario utilizar un algoritmo complejo, y es preferible uno de fácil implementación. Una cantidad muy grande puede hacer prohibitivo utilizar un algoritmo que requiera de mucha memoria adicional.

¿Qué tipo de datos quiere ordenar? Algunos algoritmos sólo funcionan con un tipo específico de datos (enteros, enteros positivos, etc.) y otros son generales, es decir, aplicables a cualquier tipo de dato.

¿Qué tamaño tienen los registros de la lista? Algunos algoritmos realizan múltiples intercambios (burbuja, inserción). Si los registros son de gran tamaño estos intercambios son más lentos.

El contenido de esta página esta basado en el material disponible en:

• http://allhost.cl/datos/
• http://www.fing.edu.uy/inco/cursos/prog1/teorico/

INGENIERO NESTOR DIAZ
FIET - UNICAUCA
2005