
DESCRIPCIÓN DEL
CURSO
El cálculo III ( cálculo en varias variables ) se
puede considerar como un curso de cálculo medianamente avanzado, de suma
importancia en los programas de Física, Matemática, Ingeniería y economía. Para
cada uno de estos campos se pueden encontra aplicaciones relacionadas directa o
indirectamente con los temas aquí tratados; sin embargo, sólo a lo largo del
desarrollo de cada una de estas carreras, el estudiante podrá incorporar en la
práctica los conocimientos aquí adquiridos.
Para obtener un buen resultado de este curso, es
indispensable que el estudiante posea un buen manejo de las herramientas
proporcionadas en los cursos de cálculo I, cálculo II y álgebra lineal, así
como la capacidad de abstraer objetos que no se pueden representar en dos o
tres dimensiones o inclusive representar mentalmente aquellos objetos posibles
de hacerlo.
En general, el cálculo es el estudio de los límites
de las funciones, y de todo lo relacionado con ellos: derivadas, integrales,
sucesiones y series.
En este curso en particular, estudiaremos los
límites de funciones llamadas campos vectoriales . Primero cuando m>1 y n=1, con
las funciones vectoriales de variable real
(
. Primero cuando m>1 y n=1, con
las funciones vectoriales de variable real
(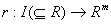 ) , luego cuando m=1
y n>1, osea las funciones escalares de variable
vectorial o simplemente funciones de varias variables (
) , luego cuando m=1
y n>1, osea las funciones escalares de variable
vectorial o simplemente funciones de varias variables (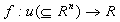 ) y finalmente en el cálculo vectorial integraremos las dos
funciones con teoremas como el teorema de Green, el
teorema de la divergencia y el teorema de stokes,
entre otros
) y finalmente en el cálculo vectorial integraremos las dos
funciones con teoremas como el teorema de Green, el
teorema de la divergencia y el teorema de stokes,
entre otros
OBJETIVOS
GENERALES
1.
Ayudar
a formar al estudiante como un individuo útil a la sociedad.
2.
Fomentar en el alumno la
investigación y la disciplina del autoaprendizaje.
3.
Mostrar
al estudiante la utilidad del cálculo de los campos vectoriales en su propia
carrera y en carreras afines.
OBJETIVOS
ESPECÍFICOS
1. Recordar los conceptos de cálculo en una variable.
2. Aprender a manejar las herramientas necesarias para calcular límites,
derivadas e integrales de campos vectoriales
3. Conocer los gráficos, ya
sean hechos a mano o por computadora, de algunos campos vectoriales, y aprender
a realizarlos
4. Modelar matemáticamente, usando los conceptos vistos a través del
curso, algunos problemas propios de la carrera y resolverlos, de ser posible
CONTENIDO DEL CURSO
CAPITULO
I FUNCIONES
VECTORIALES
1.1
Vectores: coordenadas
cartesianas en el plano y en el espacio. Vectores. Operaciones entre vectores .
Rectas y planos
1.2
Funciones vectoriales:
límites y continuidad. Derivadas y sus propiedades. Integrales y sus
propiedades
1.3
curvas y movimiento en el espacio: Rectas tangentes. Velocidad y
aceleración. Curvatura en el plano y en el espacio. Plano oscilador
CAPITULO II. LA DERIVADA EN EL ESPACIO N-DIMENSIONAL
2.1
Superficies
cuadráticas y sólidos de revolución
2.2
Funciones
de dos o más variables: Límites y continuidad Derivadas parciales
2.3
Diferenciabilidad
2.4
Derivadas
direccionales y gradiente
2.5
Regla
de la cadena
2.6
Planos
tangentes y aproximaciones
2.7
Máximos
y mínimos
2.8
Multiplicadores
de Lagrange
CAPITULO III La
INTEGRAL en el espacio n-dimensional.
3.1
Integrales
dobles sobre rectángulos
3.2
Integrales
dobles sobre regiones mas generales
3.3
Integrales
iteradas
3.4
Integrales
dobles en coordenadas polares
3.5
Aplicaciones
de las integrales dobles. Área de superficies
3.6
Integrales
triples en coordenadas cartesianas, cilíndricas y esféricas
CAPITULO IV CÁLCULO
VECTORIAL.
4.1
Campos
vectoriales
4.2
Integrales
de línea
4.3
Independencia
de la trayectoria
4.4
Teorema
de Green en el plano
4.5
Integrales
de superficie
4.6
Teorema
de divergencia de Gauss
4.7
Teorema
de Stokes
4.8
Problemas
de aplicación
EVALUACIÓN
El tipo de evaluación y la
respectiva ponderación deben ser concertadas, el primer día de clase, con los
estudiantes y teniendo en cuenta el reglamento estudiantil de la universidad
del Cauca.
BIBLIOGRAFÍA
1.
LEITHOLD,
Louis. El Cálculo con Geometría
Analítica.
El código con el cual se encuentra en la biblioteca
central es: 515. 15 L533.
2.
Purcell
E.-Varberg Dale. Cálculo con Geometría Analítica. Ed. Prentice Hall Hispanoamericana S.A., sexta
edición 1992
El
código con el cual se encuentra en la biblioteca central es: 515.15 P985
3.
PISKUNOV,
N. Cálculo Diferencial e Integral.
El código con el cual se encuentra en la biblioteca
central es: 515.3P677.
4.
PINZON,
Alvaro. Cálculo Integral.
El
código con el cual se encuentra en la biblioteca central es: 515.4076 .
5.
APÓSTOL,
Tom, M. Calculus. Volumen I y II. Ed.
Reverté.
El código con el cual se encuentra en la biblioteca
central es: 515.1A645.
6.
SALAS,
HILLE. Calculus. Volumen I y II, 2ª Edición
El código con el cual se encuentra en la biblioteca
central es: 515 S161.
7.
SWOKOWSKJ, Earl W. Cálculo con Geometría Analítica, 2ª Edición
El código con el cual se encuentra en la biblioteca
central es: 515. 150 76S979.
8.
LARSON,
Roland E. Cálculo y Geometría Analítica,
Volumen I, 6ª Edición.
El código con el cual se encuentra en la biblioteca
central es: 515. 15 L334.