APLICACIÓN DE LA TEORÍA DE GRAFOS EN LA CONTABILIDAD[*]

GUILLERMO CUELLAR MEJÍA

Universidad Sur Colombiana Neiva

INTRODUCCIÓN

La teoría de la contabilidad para muchos contadores y para  profesionales de otras disciplinas se ha enmarcado dentro del molde rígido y tradicional de la Dualidad Económica o Partida Doble. La contabilidad clásica semeja, en su evolución histórica a la lógica aristotélica. Ambas se desarrollan a lo largo de cincuenta, ochenta o cien años y luego permanecen estancadas jurante muchos siglos, sin que nadie se atreva a reemplazarlas, sino que por el contrario, se les tiene por Insustituibles para un grupo profesional (clero, comerciantes). Pero esto se debe a que se ha querido conservar v no a que no exista nadie capaz de superarlas. Es en 1957 cuando Richard Mattessich introduce la axiomática, métodos matriciales y la teoría de la medida contable para iniciar así el desarrollo de la NUEVA CONTABILIDAD que abre insospechadas perspectivas a nuestra profesión. En España Enrique Ballesteros presenta estos métodos modernos, en especial La Teoría de Grafos, estableciendo de esta manera los principios de una teoría de la objetividad y habilidad contables, asentada sobre bases diferentes a la estadística.

Se pretende con el presente trabajo, demostrar como una teoría estudiada por el genio más prolífico de la historia de las matemáticas, L. EULER (1707-1783), puede ser aplicada a la contabilidad, para así mirar a nuestra disciplina desde una óptica diferente a la antiquísima partida doble. También se busca demostrar que la contabilidad puede ser encuadrada perfectamente en un modelo matemático, la cual contribuye a reafirmar la cientificidad de nuestra profesión y negar de paso la falsa concepción que está solamente basada en simple empirismo.

Se ha demostrado que la Teoría de Grafos es una herramienta básica en muchos campos de la ciencia y la tecnología; sus teoremas y métodos han sido aplicados con éxito en temas tan diversos como teoría de la información, planificación de la producción, transportes programación lineal, redes de conexión, mecánica estadística, genética y química, encontrándosele ahora un nuevo campo de aplicación: la Contabilidad.

La aplicación de la Teoría de Gratos a la contabilidad nos conduce a la contabilidad matricial, donde el viejo concepto de partida doble desaparece, sin derrumbar las estructuras de la contabilidad al cual nos habíamos acostumbrado y que han permanecido durante siglos.

APLICACIÓN DE LA TEORÍA DE GRAFOS A LA CONTABILIDAD

Conceptos básicos de la Teoría de Grafos.

La teoría de grafos es una teoría perteneciente al álgebra moderna según la cual se estudian conjuntos de segmentos de línea v de puntos de un plano.

Su diferencia con la geometría euclidiana radica en que la teoría de gratos carece de métrica, pues la conceptualización de "distancia" se obvia para hacer generalizaciones sobre las figuras o gratos. Es así como para la teoría de grafos la línea recta y la curva son equivalentes, una figura compuesta por segmentos rectilíneos es equivalente a la misma figura compuesta por segmentos de arco, todos los triángulos son equivalentes (equilátero, escaleno e isósceles) ya que la teoría de grafos, sólo se ocupa de una propiedad común de los mismos: la triangularidad.

La teoría de gratos considera que las figuras se han dibujado en un plano "elástico", es decir supone que las figuras geométricas están representadas en una hoja delgada, altamente flexible y elástica, de modo tal que puede ser sometida a distorsión (estiramiento, retorcimiento) interesándose solamente por las propiedades que mantienen las figuras después de las deformaciones a que han sido sometidas. Obviamente la distancia entre los puntos y las formas de los segmentos han cambiado, pero el número de puntos y sus relaciones no.

Como ya se dijo, en la teoría de grafos existen dos tipos de elementos que combinados entre si forman un grafo: segmentos de línea y puntos. La teoría de grafos no se limita solamente a la representación geométrica de líneas y puntos, sino que en el campo de la información se ha dado aplicación a la programación y a la recuperación de datos, considerando que los puntos son elementos de una colección y las líneas relaciones existentes entre los elementos de la misma.

Es así como un archivo de datos, puede ser representado por un grafo: los puntos serán los registros y las líneas serán las relaciones existentes entre los registros.

De las tantas relaciones que pueden existir entre los registros, puede considerarse que la relación de ORDEN es la más importante y el grafo nos mostrará entonces como están ordenados los registros dentro del archivo.

El concepto de DIRECCIÓN es de suma importancia dentro de la teoría de gratos, para indicar el tipo de relación existente entre los puntos. La dirección se indica simplemente con una flecha sobre la línea. Es así como se tienen grafos no orientados y grafos orientados.

Los grafos no orientados o simplemente grafos son aquellos en que las líneas no tienen dirección y corresponden a grafos con relaciones simétricas, es decir, es indiferente el elemento que se menciona primero. Ejemplo: dados los elementos PEDRO y JUANA y la relación simétrica "familiar de" es indiferente si se dice "PEDRO es familiar de JUANA" ó " JUANA es familiar de PEDRO", pero si consideramos los mismos elementos pero la relación asimétrica "hermana de" encontramos que aunque JUANA es hermana de PEDRO, PEDRO no es hermana de JUANA.

Este último grafo será un grafo orientado va que la relación tiene una dirección. La línea que une dos puntos de un grafo se denomina arista en el no orientado y arco en el orientado.

Otras relaciones asimétricas tales como "padre de", "hijo de", "menor que" se representarán siempre con líneas con dirección. Para la aplicación de la teoría de Grafos a la Contabilidad, utilizaremos solamente grafos orientados.

Un grafo puede representar todas las relaciones del mismo tipo que existan entre unos elementos. Pero entre estos mismos individuos pueden existir otros tipos de relaciones y cada uno representarse con un grafo. Ahora bien, existe un problema ¿cómo se pueden superponer geométricamente estos gratos?

Una solución puede ser utilizar líneas de colores diferentes, para indicar cada relación.

Otra solución es la de emplear trazos diferentes para cada relación (trazo delgado, grueso, punteado, etc.).

En el presente trabajo usaremos este último método en razón a las limitaciones en el uso del color.

TEORÍA DE GRAFOS Y CONTABILIDAD

Para aplicar la teoría de grafos a la contabilidad consideraremos que los elementos de la colección son las cuentas del sistema contable y las relaciones entre los elementos son las transferencias de recursos entre las cuentas.

Así deberemos entonces concebir que la representación de una cuenta será un punto en el papel, en el cual deberán marcarse tantos puntos como cuentas del sistema se utilicen, los cuales serán C₁ C₂, C₃.... Cn (Figura 2).

La propiedad general de las cuentas se definirá así: Desde una cuenta X_i a otra cuenta X_j se pueden transferir recursos, tales como dinero, mercancías, bienes económicos y derechos legales debidamente medidos en unidades monetarias.

Para representar una transferencia de recursos desde C_i a C_j, se trazará en el plano una línea, orientada (arco) desde C_i a C_j. Encima de cada arco se escribirá una cifra, N_ij, que indique la medida en unidades monetarias de la transferencia. Esta cifra será la relación entre las dos cuentas y se denominará número asociado al arco.

El modelo general para representar una transacción contable lo podemos observar en el grafo de la Figura 3.

Utilizaremos la Figura 3 para definir algunos términos y propiedades de los grafos así:

Los puntos C₁ C₂, C₃.... Cn poseen una propiedad: de ellos no salen ni llegan líneas, entonces se dice que son puntos aislados.

Los puntos C_i y C_j poseen una propiedad también: la conexión, la cual existe cuando entre dos puntos de un grafo hay una línea (camino).

Los puntos conectados por un arco se denominan vértices. El punto del que parte la flecha (C_i) se denomina vértice inicial y el punto donde termina (C_j) vértice final.

La línea que une a Ci con Cj se denomina Arco (A_ij) y la cifra N_ij indicará el valor de la transferencia realizada de C_i a C_j.

Para comprender el modelo supondremos el siguiente ejemplo:

Se organiza la sociedad La Gráfica Ltda. con un capital de 110 millones de pesos, representado por 10 millones de pesos en efectivo, 20 millones en maquinaria y 80 millones de un edificio.

Construiremos el grato contable de la anterior transacción así:

1.

Se transfiere dinero en efectivo de los socios a la sociedad (10 millones). Denominaremos C₁ a la cuenta CAPITAL la cual representa los derechos de los socios en la sociedad, y C₂ a la cuenta EFECTIVO que representa el dinero de la sociedad tanto en Caja como en Bancos. Trazamos un arco A₁₂ desde el vértice C₁ al vértice C₂, orientado hacia C₂ (la flecha apunta a C₂).

2.

Se transfieren máquinas y equipos de los socios a la sociedad por valor de 20 millones. Denominamos C₃ a la cuenta MAQUINARIA. Nuevamente se traza un arco A ₁₃ desde C₁ (CAPITAL) a C₃ (MAQUINARIA) con la flecha indicando a C₃.

3.

La transferencia del edificio tiene idéntico tratamiento. Se denota el vértice C₄ como EDIFICIOS y se traza un arco A ₁₄ desde C₁ a C₄ (EDIFICIOS) orientado hacia C₄.

4. Escribimos sobre cada arco trazado el número asociado al mismo que es el valor de cada transferencia, representándose así el grafo contable de la constitución de la sociedad La Gráfica Ltda. (Figura 4).

Consideremos que a La Gráfica Ltda. le concede un crédito el Banco ABC por 5 millones, compra mercancías por 2 millones al contado y realiza venta de una máquina recibida de los socios por 5 millones.

Para graficar las entradas y las salidas de recursos en teoría de grafos pueden utilizarse dos métodos:

a. Utilizar dos arcos, uno para los recursos que llegan al vértice y otro orientado inversamente para los recursos que salen.

b. Emplear un solo arco usando como número asociado al arco la diferencia entre los recursos recibidos a y los transferidos.

Para la aplicación a la contabilidad es más útil usar el primer método. (Ver figura 5).

Para seguir adelante en la aplicación de la teoría de grafos, se hace necesario introducir el concepto de flujo.

Un grafo es atravesado por un flujo cuando cumple las siguientes propiedades:

1. El grafo posee un vértice único del cual salen arcos, pero al que no llegan arcos (vértice inicial).

2. El grafo posee un vértice único al cual llegan arcos pero del que no parten arcos.

3. En cualquier vértice V_i, la suma de los números asociados a los arcos que llegan a V_i, es igual a la suma de los números asociados a los arcos que salen de V_i (la suma algebraica de los números asociados a los arcos que llegan y los arcos que salen de V_i es cero).

En el grafo contable de la Figura 5, no pasa un flujo pues no cumple las dos primeras propiedades, pero sí la tercera, esto se explica en razón a que las cuentas no están saldadas. Para que cumpla las dos primeras condiciones se debe modificar en forma convencional introduciendo dos vértices ficticios C_a y C_n.

Analizando el grafo de la Figura 5 y aplicando la propiedad descrita en el punto 3 tenemos:

Para el vértice C₁    CAPITAL

O - (10 + 20 +80) =  -110

Para el vértice C₂ EFECTIVO

(10 + 5 + 5) - 2 = 18

Para el vértice C₃  MAQUINARIA

20 - 5 = 15

Para el vértice C₄  EDIFICIOS

80- O = 80

Para el vértice C₅ OBLIG. BANCARIAS

O - 5 = -5

Para el vértice C₅  ALMACÉN

2 - O = 2

La fórmula aplicada es:

Para hacer pasar un flujo por el grafo de la Figura 5 se procede de la siguiente manera:

a) Introducimos dos vértices C_a y C_n.

b) Si un vértice cualquiera presenta una diferencia negativa, se traza un arco con línea gruesa, desde Ca hasta el vértice en cuestión, orientada la línea hacia dicho vértice y anotando encima del arco el importe de la diferencia como número asociado al arco.

c) Si un vértice cualquiera presenta una diferencia positiva, se traza un arco con línea gruesa desde el vértice en cuestión hasta Cn con orientación hacia Cn, colocándose encima del arco la cifra de la diferencia como número asociado al arco.

El grafo de la Figura 5 queda convertido en el grafo mostrado por la Figura 6.

La operación que se ha realizado consistió en hacer pasar un flujo por el grafo.

Esto produjo el hecho de saldar las cuentas obteniéndose el Balance General o Estado de Posición Financiera así:

Las cuentas de Derechos (Activo) serán todos los vértices cuyos Arcos de trazo grueso se encuentren orientadas hacia el vértice C y su saldo será el número asociado a cada arco. Las cuentas de Obligaciones (Pasivo) serán todos aquellos vértices que posean arcos en trazo grueso provenientes del vértice C. Entonces, tenemos que la posición financiera de "La Gráfica Ltda.” estará dada de la manera siguiente:

Asientos Compuestos, un problema que se presenta al aplicar la teoría de gratos a la contabilidad, es el de los asientos múltiples o compuestos. Para resolverlo se hace necesario la utilización de un vértice "puente" o vértice "comodín".

Para ejemplificar supondremos la siguiente transacción:

Se adquiere una empresa por valor de 64 millones la cual consta de un edificio que tiene un valor de 30 millones, el terreno con valor de 10 millones y maquinaria por valor de 24 millones. La operación se paga así: en efectivo se pagan 12 millones, se firman letras a un año por 17 millones y el resto con hipoteca a 15 años.

Contablemente se deberá efectuar el siguiente asiento:

El grafo contable del anterior asiento compuesto necesita utilizar un vértice puente ó comodín para mostrar la transferencia de recursos entre las diferentes cuentas y quedaría representado por el grafo de la Figura 7.                                          

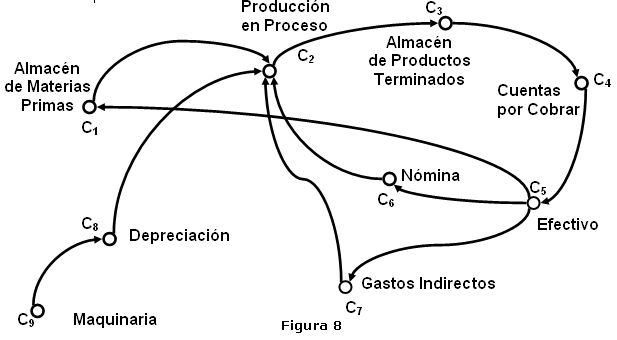
El grafo de la Figura 8 representa la transferencia de recursos que constituyen el Costo de Producción de un artículo y en él se aprecian los conceptos descritos anteriormente, así:

Los vértices C₁, C₂, C₃, C₄ constituyen un camino.

Otros caminos serían los formados por los vértices C₄, C₅. C₆ y C₂; C₅, C₇ y C₂ y el formado por los vértices C₉, C₈ y C₂.

Un circuito sería el formado por los vértices C₂, C₃, C₄, C₅, C₆ y C₂, ya que el vértice inicial y final es C₂.

Otros caminos serían los formados por los vértices C₁, C₂, C₃, C₄, C₅ y C₁ y el conformado por los vértices C₂, C₃, C₄. C₅. C₇ y C₂.

Como se puede observar el asiento compuesto se representó en el grafo mediante el artificio de introducir el vértice comodín C₄ el cual permite mostrar la transferencia de recursos que de otra manera no sería posible.

Aunque por razones de limitaciones de espacio no es posible mostrar en este trabajo todas las aplicaciones de la teoría de gratos a la contabilidad, presentaremos en forma sucinta otros conceptos de plena utilización.

Camino. Se llama camino a una secuencia de arcos simple, es decir en la que ningún arco se repite y se encuentran orientados en el mismo sentido.

Circuito. Se llama circuito a una secuencia de arcos (camino), que comienza y termina en el mismo punto.

Otras aplicaciones dentro de la Contabilidad

La teoría de gratos puede tener también aplicación dentro de los presupuestos a través de los Flujos Presupuestales. Para tal efecto se trazará un grafo, cuyos arcos representen los asientos de Diario por período presupuestado, dibujándose los arcos sin asignarles números asociados. Es posible establecer cuál será la magnitud de cada arco de manera aproximada considerando:

a. Para cada cuenta (vértice) se sabe cuál será su saldo.

b. Para cada arco se estima su capacidad, si se entiende a ésta como el máximo número que puede asociarse al arco.

c. Se debe definir cuál es el presupuesto óptimo de acuerdo al objetivo de la empresa.

CONTABILIDAD MATRICIAL

La aplicación de la Teoría de Gratos a la contabilidad, nos permite conceptualizar la antigua partida doble como una matriz cuadrada con un número C de columnas y un número F de filas, donde C = F ya que existirá una tila y una columna por cada cuenta.

Esta matriz tendrá C*T elementos y el número máximo de relaciones entre las cuentas estará dado por (C*F) -C ó (C*F) -F. es decir el número total de elementos de la matriz menos el número de cuentas o vértices involucrados. Esto se entiende perfectamente si observamos que una cuenta o vértice no puede tener relaciones consigo mismo, o lo que es lo mismo su relación siempre tendrá un número asociado con valor cero.

Hecha esta explicación, el modelo de la contabilidad matricial estaría dado como sigue:

Este modelo matricial lo hemos desarrollado tomando como base el grafo de la Figura 5 en el cual existían seis vértices o cuentas, lo que obviamente produce una matriz cuadrada de seis columnas por seis filas, con 36 elementos o relaciones de las cuales seis tendrán siempre un valor de cero por ser la intersección de cada cuenta con sí misma, lo que nos da un número máximo de 30 relaciones entre estas cuentas.

Para convertir un grafo en una matriz, debemos considerar que a cada arco A_ij del grafo le corresponde un elemento m_ij de la matriz y su valor será el del número asociado al arco A_ij. Si no existe número asociado al arco, es obvio que no hay relación entre los vértices y por tanto su valor será cero. Cuando en un elemento m_¡j se tiene que i = j, entonces su valor será siempre cero ya que se trata de la relación de la cuenta con sí misma.

Aplicando estos conceptos al grafo de la Figura 5, tenemos que entre el vértice C₁ (CAPITAL) y el vértice C₂ (EFECTIVO), existe un arco A₁₂ con un número asociado de 10 millones que nos da origen al elemento m₁₂ el cual tendrá un valor de 15 millones. Así mismo el arco A₁₃ dará origen al elemento m₁₃ con valor de 20 millones; el arco A₁₄ al m₁₄ con valor de 80 millones; el arco A₂₆ al elemento m₁₄ con valor de 2 millones; el arco A₅₂ al elemento m₅₂ con valor de 5 millones y el arco A₃₂, da origen al elemento m₃₂ por 5 millones. Trasfiriendo todo lo anterior a la matriz M tendremos lo siguiente:

Esta matriz M_i nos está mostrando el movimiento de las cuentas en un momento dado. Para entenderlo mejor debemos señalar que bajo este modelo las columnas representan los DÉBITOS y las filas los CRÉDITOS. La sumatoria de los elementos de una columna se denomina VECTOR DEBE y la sumatoria de los elementos de una fila VECTOR HABER. La diferencia entre el VECTOR DEBE y el VECTOR HABER se denomina VECTOR DE SALDOS.

Hasta el momento solamente hemos desarrollado la matriz M_i a partir de un grafo, pero no hemos explicado cómo sería la mecánica de la contabilidad matricial. Para este efecto consideraremos a M_i como la matriz inicial de mayor y desarrollaremos matrices de diario D para ejemplarizar el movimiento contable de un período, advirtiendo que al aparecer nuevas cuentas deberá ampliarse la matriz M para adicionar las columnas y filas que se necesiten.

Supondremos que se realizan las siguientes transacciones: se adquieren Muebles y Enseres por valor de 4 millones pagándose 1 millón al contado y el saldo con letras. Se cancelan Gastos Generales en efectivo por valor de 1 millón. Se compra un vehículo por 6 millones, cancelándose 2 millones en efectivo y el saldo firmando documentos.                            

Dado estos supuestos hallamos que se deben abrir nuevas cuentas y por tanto se debe ampliar la matriz con los vértices siguientes:

C₇ MUEBLES Y ENSERES

C₈ DOCUMENTOS A PAGAR

C₉ GASTOS GENERALES

c₁₀ VEHÍCULOS

Ahora si se procede a desarrollar una matriz D por cada una de las operaciones así:

1. Por la compra de Muebles:

Este es un típico asiento compuesto en donde se ha dividido el total del cargo a C₇ MUEBLES Y ENSERES para afectar las otras cuentas involucradas (C₂ EFECTIVO y C₈ DOCUMENTOS A PAGAR).

2. El pago de Gastos Generales:

3. Por la adquisición del Vehículo:

Otro caso de asiento compuesto al cual se le da él tratamiento idéntico al del asiento 1.

Después de realizadas las matrices de Diario, debemos mayorizarlas, es decir sumar las matrices D₁, D₂ y D₃ a la matriz M_j para obtener la matriz M_f o sea la matriz final del Mayor quedando representada de la siguiente manera:

Debemos ahora proceder a obtener los saldos de cada cuenta, sumando las columnas para obtener el VECTOR DEBE y sumando las filas para encontrar el VECTOR HABER y posteriormente determinar el VECTOR SALDO así:

De donde obtenemos lo siguiente:

Una vez obtenido el VECTOR SALDO se forma el VECTOR BALANCE, simplemente creando dos conjuntos: los saldos positivos que conformarían los DERECHOS ACTIVOS) y los saldos negativos que conformarían las OBLIGACIONES (PASIVOS).

De todo lo anteriormente expuesto podemos observar que la contabilidad matricial implica una simplificación de la partida doble tradicional pues esta última se reduce a anotar valores en la intersección de las cuentas involucradas en un asiento contable.

CONCLUSIONES

Es posible desarrollar un modelo contable diferente del archiconocido método de La Partida Doble, utilizando una rama de las Matemáticas Modernas: La Teoría de Grafos.

La contabilidad así desarrollada, consistiría en una representación gráfica de la medición de un hecho económico valorado en unidades monetarias. La aplicación práctica de la Teoría de Gratos sería demasiado engorrosa y de poca utilidad en razón a que debido a las múltiples operaciones de la empresa se haría necesario trazar una gran cantidad de arcos y números asociados a los mismos, resultando entonces una falta de claridad o falta de datos.

Sin embargo, la introducción de la Teoría de Grafos a la contabilidad nos demuestra que es posible representar un asiento contable simple por medio de una abstracción de tipo matemático, considerando a las cuentas como elementos de un conjunto y a las transacciones como las relaciones entre los elementos de ese conjunto, lo cual sería de gran utilidad en la enseñanza de la contabilidad, pues se quitaría gran parte de la mecánica existente en la Teneduría de Libros y se le daría un carácter más analítico a la misma, desarrollándose así la capacidad analítica que debe poseer todo Contador Público.

Por otra parte, la Teoría de Grafos, nos permite introducimos en la Contabilidad Matricial, la cual puede ser utilizada ampliamente en la práctica, si se considera que las Matrices Electrónicas (Visicalc, Lotus 123, Lotus Simphony, Multiplan. Supercalc. etc.) permiten a través de sus poderosas funciones, desarrollar un modelo contable sencillo que produciría los resultados deseados por el Contador (Estado de Posición Financiera, Estado de Resultados). Este Modelo Contable sistematizado electrónicamente, aunque carece de algunas utilidades de un sofisticado programa contable, cumpliría con muchos de los requerimientos de información para la empresa, con la ventaja de su bajo costo y del hecho que el mismo contador puede diseñarlo a su gusto, sin necesidad de poseer profundos conocimientos de programación y diseño de sistemas.

Es de anotar que usando el concepto de Contabilidad Matricial, personalmente he diseñado modelos contables los cuales me han sido de gran utilidad práctica en la obtención de información financiera de varias empresas, a través de la Matriz Electrónica LOTUS 123.

BIBLIOGRAFÍA

BALLESTEROS. Enrique. LA NUEVA CONTABILIDAD. Alianza Editorial. Madrid.

BERGE. C. THE THEORY OF GRAPHS. Methuen & Co. Ltd. BUSACKER. R. G and  SAATY. T. L FINITE GRAPHS AND NETWORKS. Mc. Graw Hill.

DEL RIO GONZÁLEZ. Cristóbal. HETERODOXIA CONTABLE. Ecasa México. 1983.

FLORES. Iván. ESTRUCTURACIÓN Y PROCESO DE  DE DATOS. Tomo 4.

TÉCNICAS DE INFORMÁTICA HOY. Paraninfo. Madrid. 1982.

TURNER. J C. MATEMÁTICA MODERNA APLICADA. Alianza Editorial. Madrid. 1970.